|
Joint
Critical Thinking Project via Modeling Linear Functions Using Temperature
Conversion Scales |
|
Abstract: At FSCJ exercises
are being developed to demonstrate critical thinking ability of the students.
This project is a joint effort to compare students in both College Algebra
and Chemistry classes. The functional relationship between the Fahrenheit and
Celsius Temperature scales are derived using the corresponding boiling and
freezing points of water. In this project students each create a unique
Temperature scale using the student’s body weight and the student’s age as
the boiling and freezing points of water respectively. This “student” scale
is then compared to the Fahrenheit and Celsius scales. The resulting
functions are graphed and compared. We will illustrate this on the webpage:
http://www.lsua.info/mathworkshop1/frametemp2.html |
|
Complete Description: At FSCJ exercises are being developed to demonstrate
critical thinking ability of the students in all of the general education
classes. Cognitive scientists define “critical thinking” as mental activity
associated with these types of thinking: a. applying reasoning; b. making
decisions; c. problem solving. This critical thinking project is a joint
effort to compare students in both College Algebra and Chemistry classes. The actual project handout follows on the next several
pages: |
CHM 1025C/MAC 1105: Critical Thinking Exercise
By definition:
Learning - the acquisition of knowledge or skill.
Teaching – the action of a person who is showing or helping a person to learn.
Cognitive scientist define “critical
thinking” as mental activity associated with these types of thinking:
a. applying reasoning
b. making decisions
c. problem solving
In the CHM 1025C Corwin textbook used at Florida State College @ Jacksonville , critical thinking is introduced within the context of chemical principles. In CHM 1025C and the Corwin text critical thinking is undertaken specifically in the chapter vignette and end-of-chapter self-tests, and generally in unit analysis problem solving.
In the CHM 2045C MvMurry’s textbook used by the instructor at North Campus, critical thinking is not introduced or discussed.
At FSCJ we have been addressing “Institutional Effectiveness”(I.E) across the curriculum. The faculty is developing district wide exercises to assess learning outcomes. For chemistry (CHM 1025C) the science council/cluster feels we need to pursue under our course goals and objectives the following outcomes:
FSCJ CHM 1025C Official
Learning Outcomes:
1. Explain and apply major concepts in general
chemistry
2.
Demonstrate
knowledge of scientific method
3.
Interpret scientific models such as formulas, graphs, tables
and schematics, draw inferences from
them and recognize their limitations.
4.
Demonstrate problem solving methods
in situations that are encountered outside of the classroom
The following lab exercise addresses all four of the above, especially #3:
Lab Assignment #12:
CHM 1025C Students: Read Corwin’s Section 2.9:
Temperature
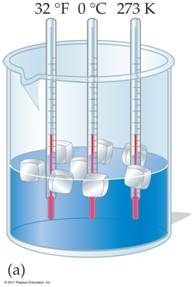
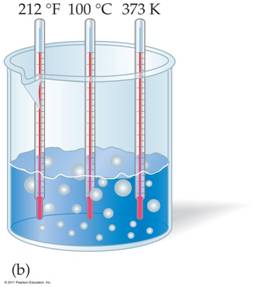
The above images from Chapter 2 of the CHM 1025C Corwin textbook(page 51) or the below image from Chapter 1 McMurry’s CHM 2045 textbook (page 13) demonstrate equivalent temperatures on the Fahrenheit and Celsius scales with ice water and boiling water. The third thermometer compares to Kelvin Temperatures to Fahrenheit and Celsius temperatures. McMurry just shows the 3 thermometers.
CHM 2045C Students: Read McMurry’s Section 1.8: Temperature 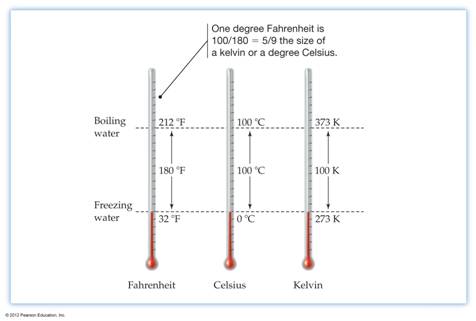
Go to the temperature conversion web site: http://www.lsua.info/mathworkshop1/frametemp2.html
- Setup the Student’s theoretical temperature scale with the following parameters:
A. The Freezing
Point of water is Your Age or Your desired Age. (Prof Taylor 50oT)(Ms Sweet 30oS)
B. The Boiling Point of water
is your body weight or desired body weight (Prof Taylor 250oT)(Sweet 120oS)
- Fill in the table below/next
page with your parameters to make oX (Student): (Professor
Taylor’s normal body temperature is the normal 98.6 oF,
Professor Bessman 96.8 oF, and Ms Sweet 97.3 oF.
- If your normal body
temperature is not 98.6 then fill in you Fahrenheit temperature and
calculate the blanks across the line of the table for at least 5 points
from +250oF to -150oF
Table
of Equivalent Temperatures:
|
Temperature oF |
Temp.
oC |
Temp.
K |
Temp.
oT |
Temp.
oS |
Temp.
oX |
|
(Fahrenheit) |
(Celsius) |
(Kevin) |
(Taylor) |
(Sweet) |
(Student) |
|
250 |
121 |
394 |
298 |
139.0 |
|
|
212 |
100 |
373 |
250 |
120.0 |
|
|
158 |
70 |
343 |
190 |
93.0 |
|
|
104 |
40 |
313 |
130 |
66.0 |
|
|
|
|
|
|
|
|
|
98.6 |
37.0 |
310.0 |
124.0 |
63.3 |
|
|
|
|
|
|
|
|
|
97.3 |
36.3 |
309.3 |
122.6 |
62.7 |
|
|
|
|
|
|
|
|
|
96.8 |
36.0 |
309.0 |
122 |
62.4 |
|
|
81 |
27 |
300 |
104 |
54.5 |
|
|
77 |
25 |
298 |
100 |
52.5 |
|
|
75 |
24 |
297 |
98 |
51.5 |
|
|
68 |
20 |
293 |
90 |
48.0 |
|
|
50 |
10 |
283 |
70 |
39.0 |
|
|
32 |
0 |
273 |
50 |
30.0 |
|
|
14 |
-10 |
263 |
10 |
21.0 |
|
|
0 |
-18 |
255 |
1 |
14.0 |
|
|
-4 |
-20 |
253 |
-2 |
12.0 |
|
|
-22 |
-30 |
243 |
-14 |
3.0 |
|
|
-28 |
-33.3 |
240 |
-17 |
0.0 |
|
|
-40 |
-40 |
233 |
-26 |
-6.0 |
|
|
-58 |
-50 |
223 |
-33 |
-15.0 |
|
|
-76 |
-60 |
213 |
-50 |
-24.0 |
|
|
-130 |
-90 |
183 |
-86 |
-51.0 |
|
|
-148 |
-100 |
173 |
-98 |
-60.0 |
|
- Using a rectangular piece
of graph paper, set up a graph plotting Fahrenheit versus Celsius so that
vertical axis is Fahrenheit ranging from 250 down to -150 and the
horizontal axis is -100 on the left and 125 on the right.
a. Describe the line or curve generated by this data:
b. If the plot is a line, then what is the slope of the line and the Y intercept and the X intercept.
c. Write the equation
for the line.(Do you remember the equation of a straight line from
algebra?)
d. If the plot is a curve, can you write the equation of the curve?
- Now plot Celsius versus Kelvin on a rectangular coordinate graph. If Kelvin is the y axis and Celsius is the x axis, where should the data point (0,273) be located?
- what is the y axis intercept? What is the slope of the line?
- Is there an easier way to find the slope of the line by looking at the data?
- At what temperature Celsius would Kelvin equal zero?
- In the Corwin textbook on page 50 and in the McMurry textbook on page 13 we refer to temperature on the Fahrenheit and Celsius scales as degree F (oF) and degree C (oC), but in Kelvin temperature, temperatures are referred as Kelvin units (not oK – degrees Kelvin) (the word scale is actually incorrect)? Why?
- Now plot Celsius versus Student and Fahrenheit versus Student using separate graphs. On the oC vs oF graph, examining the data do you notice that: -40 oF = -40 oC. On your two Student graph plots is there a temperature where oS = oC or oS = oF?
- Algebraically is there away to determine if there is a temperature on the Taylor Scale, the Sweet Scale, or the Student Scale when that temperature equals a temperature on either the Celsius or Fahrenheit scale? If so, on a separate piece of paper show the calculations for each (up to six).
- Algebraically is there away to determine if there is a temperature on the Celsius Scale when that temperature equals a temperature on the Kelvin scale?Why?
Sample Graph Paper

Fahrenheit versus Celsius Name:________________________

Fahrenheit versus Celsius Name:________________________

Kelvin versus Celsius Name:________________________

Kelvin versus Celsius Name:________________________

Fahrenheit versus Student Name:________________________

Fahrenheit versus Student Name:________________________

Celsius versus Student Name:________________________

Celsius versus Student Name:________________________
