CHM 1025C: Critical Thinking (page xvii) Name: ___________________
Cognitive scientist define “critical
thinking” as mental activity associated with these types of thinking:
a. applying reasoning
b. making decisions
c. problem solving
In the CHM 1025C Corwin textbook , critical thinking is introduced within the context of chemical principles. In CHM 1025C and the Corwin text critical thinking is undertaken specifically in the chapter vignette and end-of-chapter self-tests, and generally in unit analysis problem solving.
Assignment #1:
Read section 3.8: Temperature
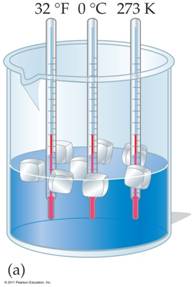
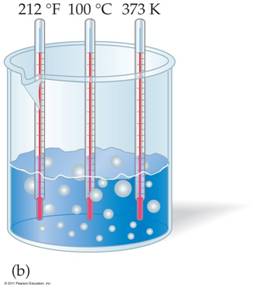
The above images demonstrate equivalent temperatures on the Fahrenheit and Celsius scales with ice water and boiling water. The third thermometer compares to Kelvin Temperatures to Fahrenheit and Celsius temperatures.
Go to the temperature conversion web site:
http://www.lsua.info/mathworkshop1/frametemp2.html
1.Setup the Student’s theoretical temperature scale with
the following parameters:
a. The Freezing Point of water is Your
Age or Your desired Age. (Prof taylor 50oT)(Ms
Sweet 30oS)
b. The Boiling Point of water is your body weight or desired body weight (Prof
Taylor 250oT)(Sweet 120oS)
c. Fill in the table
below with your parameters to make oX
(Student): (Professor Taylor’s normal body temperature is the normal 98.6 oF, Professor Bessman
96.8 oF, and Ms Sweet 97.3 oF. If your normal body
temperature is not 98.6 then fill in you Fahrenheit temperature and calculate
the bloanks across the line of the table.))
|
Temperature oF |
Temp. oC |
Temp. K |
Temp. oT |
Temp. oS |
Temp. oX |
|
(Fahrenheit) |
(Celsius) |
(Kevin) |
(Taylor) |
(Sweet) |
(Student) |
|
250 |
121 |
394 |
298 |
139.0 |
|
|
212 |
100 |
373 |
250 |
120.0 |
|
|
158 |
70 |
343 |
190 |
93.0 |
|
|
104 |
40 |
313 |
130 |
66.0 |
|
|
|
|
|
|
|
|
|
98.6 |
37.0 |
310.0 |
124.0 |
63.3 |
|
|
|
|
|
|
|
|
|
97.3 |
36.3 |
309.3 |
122.6 |
62.7 |
|
|
|
|
|
|
|
|
|
96.8 |
36.0 |
309.0 |
122 |
62.4 |
|
|
81 |
27 |
300 |
104 |
54.5 |
|
|
77 |
25 |
298 |
100 |
52.5 |
|
|
75 |
24 |
297 |
98 |
51.5 |
|
|
68 |
20 |
293 |
90 |
48.0 |
|
|
50 |
10 |
283 |
70 |
39.0 |
|
|
32 |
0 |
273 |
50 |
30.0 |
|
|
14 |
-10 |
263 |
10 |
21.0 |
|
|
0 |
-18 |
255 |
1 |
14.0 |
|
|
-4 |
-20 |
253 |
-2 |
12.0 |
|
|
-22 |
-30 |
243 |
-14 |
3.0 |
|
|
-28 |
-33.3 |
240 |
-17 |
0.0 |
|
|
-40 |
-40 |
233 |
-26 |
-6.0 |
|
|
-58 |
-50 |
223 |
-33 |
-15.0 |
|
|
-76 |
-60 |
213 |
-50 |
-24.0 |
|
|
-130 |
-90 |
183 |
-86 |
-51.0 |
|
|
-148 |
-100 |
173 |
-98 |
-60.0 |
|
2. Using a rectangular piece of graph paper, set up a graph
plotting Fahrenheit versus Celsius so that vertical axis is Fahrenheit ranging
from 250 down to -150 and the horizontal axis is -100 on the left and 125 on
the right.
a. Describe the line or curve generated by this data:
b. If the plot is a line, then what is the slope of the line and the Y intercept and the x intercept. Write the equation for the line.(Do you remember the equation of a straight line from algebra?)
c. If the plot is a curve, can you write the equation of the curve?
3. Now plot Celsius versus Kelvin on a rectangular coordinate graph. If Kelvin is the y axis and Celsius is the x axis, what is the y axis intercept? What is the slope of the line?
Is there an easier way to find the slope of the line by looking at the data?
At what temperature Celsius would Kelvin equal zero?
In the Corwin textbook on page 62 we refer to temperature on the Fahrenheit and Celsius scales as degree F (oF) and degree C (oC), but in Kelvin temperature, temperatures are referred as Kelvin units? Why?
4. Now plot Celsius versus Student and Fahrenheit versus Student using separate graphs. On the oC vs oF graph, examining the data do you notice that: -40 oF = -40 oC. On your two Student graph plots is there a temperature where oS = oC or oS = oF?
5. Algebraically is there away to determine is there is a temperature on the Taylor Scale, the Sweet Scale, the Student Scale when that temperature equals a temperature on the Celsius of fahreinheit scale?
Assignment #2: The Nine Dot Problem
Perception is often affected by unconscious assumptions. In the following problem try to connect each of the dots using four straight, continuous lines:

Here is another set:

On Page 10, Corwin Chapter 1 Problem #17: Is it possible to solve the nine dot problem with only three straight, continuous lines?

Now Try Problem#18. Is it possible to solve the nine dot problem with only one straight, continuous line?

Assignment #3: Contradiction in Perception
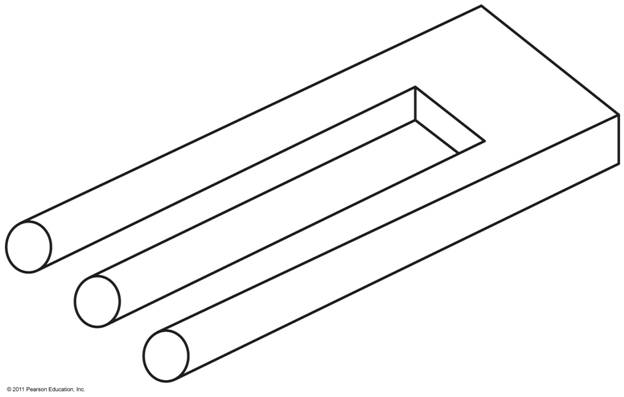
20:
Explain how the following image creates a contradiction in perception?
Assignment #4: The Nine Penny Problem
On page 33 of the Corwin textbook, there is a discussion of the metals that makeup the penny minted before 1982 and after 198. The first 1₵ coin was minted in 1793 from pure copper and was about the size of our current half dollar. This copper penny continued to be minted until 1856 when it was replaced by a penny made from a mixture of 88% copper and 12% nickel. Recently this penny sold for 1.38 million dollars:
1793
Penny: 
The addition of nickel metal gave the 1₵ coin a white appearance:
The 1857 Flying Eagle Penny


The Indian head penny 1859-1909. In 1864 the penny was changed for the 88% copper to bronze which is 95% copper and 5% zinc/tin which weighs 3.11 grams.
This bronze penny stayed in production until 1982. From 1910 to 1982 the penny was the Lincoln head penny. The design from 1920 to 1958 is known as the wheat penny . In 1959 the tails side was changed to the Lincoln Memorial cent.
In 1943 because of WWII the bronze penny was changed for one year only to a zinc coated steel penny which weighed 2.7 grams:
After 1982, the penny really became a copper coated zinc penny 97.5% zinc and 2.5% copper. This new penny weighs 2.5 grams. In 2010, the tails side of the Lincoln penny was again changed.
Now the Nine Penny Problem!
Given a two pan analytical balance:
|
|
You have nine pennies.
Eight of the pennies are post 1982 pennies (weighing 2.5 grams each). One is
a pre 1981 Lincoln penny (weighing 3.11 grams). You write a procedure so
that you can 100% of the time find the heavier Lincoln penny using the double
pan balance. |
Procedure
#1:
Possible results:
Procedure
#2:
Possible Results:




