CHM 1025C Name: _________________
Module Five II Homework Packet

Module Five Part II: Chemical Equations & Stoichiometry (Chapter 8 and 9)

A._____(05) Molecular Mass Calculation-Section8.3 Answers a

B._____(10) Mole Calculations I-Sections 8.2 old sample pretest: Answers bcd

B1.____(10) Mole Calculation II-Section 8.4 old sample pretest: Answers bcd

C._____(05) Percentage Composition Calculation-Section 8.7 old sample pretest Answers bcd

D._____(05) Empirical Formula Calc. from Lab Data-Section 8.8 old preterst Answers bcd

D1.____(05) Empirical Formula Calc. from % Comp-Section 8.8 old pretest Answers bcd

______(30) Total = ______%

M._____(50) Multiple Choice Exam Chapters 8, 9,

M-5ii Required Homework:

______(30) M-5ii Pretest Hardcopy Homework Packet (Submit on Exam#3Day)

______(25) M-5ii Multiple Choice (MC) Practice (Blackboard Online)

Module Five-Part A: Molecular Mass Calculation 5 points
The atomic mass of any substance expressed in grams is the molar mass (MM) of that substance.

• The atomic mass of carbon is 12.01 amu per atom.

• Therefore, the molar mass of carbon is 12.01 g/mol .

• Since nitrogen occurs naturally as a diatomic, N₂, the molar mass of nitrogen gas is two times 14.01 g or 28.02 g/mol.

Calculating Molar Mass

• The molar mass of a substance is the sum of the molar masses of each element.

• What is the molar mass of copper(II) nitrite, Cu(NO₂)₂?

• The sum of the atomic masses is as follows:

63.55 + 2(14.01 + 16.00 + 16.00) =

63.55 + 2(46.01) = 155.57 amu per molecule

• The molar mass for Cu(NO₂)₂ is 155.57 g/mol.

Homework:

Using a periodic chart calculate the molar mass of the following:
1. Calculate the molecular mass of Acetic Acid, HC₂H₃O₂.

2. Calculate the formula unit mass of Ammonium Chromate, (NH₄)₂CrO₄ .

3. Calculate the molecular mass of glucose, C₆H₁₂O₆.

Reference: Section 8.3

Additional Problems: #13-#16 Pages 244-245

Interactive Online Chem-i-Calc(Molar Mass & % Composition):

http://people.emich.edu/bramsay1/ccc-release/chem.html

Module Five II Homework Packet

Part B: Mole calculation 20 points

Your text has a lot of focus to convert masses and volumes to mole to actual particles. Section 8.2 (Mole Calculation I) relates the number of particles (Avagadro’s Number) to the number of moles. In Section 8.4 (Mole Calculation II) the moles are related to mass starting with the number of particles. Then vice versa. Section 8.5 defines Molar Volume. We will wait till Module 6 to do Sections 8.5 (Molar Volume) and 8.6(Mole Calculation III)

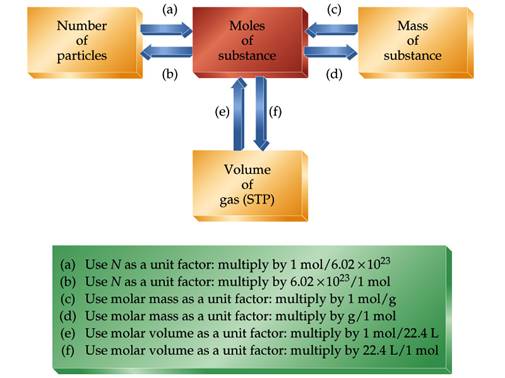
This is the only time in the course you will need to use Avogadro's number to relate actual particles to masses and volumes. In the lab we move from masses to mole and never focus on the number of particles.

What is a mole?

• The mole (mol) is a unit of measure for an amount of a chemical substance (chemist dozen).

• A mole is Avogadro’s number of particles, which is 6.02 x 10²³ particles.

1 mol = Avogadro’s number = 6.02 x 10²³ units (atoms, Molecules, ions, e^1-)

We can use the mole relationship to convert between the number of particles and the mass of a substance

Example B1: How many sodium atoms are in 0.240 mol Na?

Question : _____?______Na Atoms = 0.240 mol Na

1. We want atoms of Na.

2. We have 0.240 mol Na.

3. 1 mole Na = 6.02 x 10²³ atoms Na.

Solution:

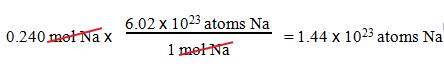
Homework #1:

B1: How many Carbon atoms are contained in 0.01667 moles of Carbon ( 1 carat diamond)?

Example B2: How many moles of aluminum are in 3.42 x 10²¹ atoms Al?

Question : _____?______Mole Al = 3.42 x 10²¹ atoms Al

1. We want moles Al.

2. We have 3.42 x 10²¹ atoms Al.

3. 1 mol Al = 6.02 x 10²³ atoms Al.

Solution:

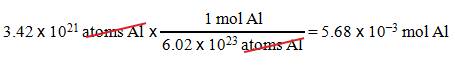
Homework #2:

B2: How many moles of Carbon are contained in 3.016 x 10²² atoms of Carbon (3 carat diamond)?

Part B: Mole calculation II 10 points

We will be using the unit analysis method again.

Recall the following steps:

Mole Calculations II

Now we will use the molar mass of a compound to convert between grams of a substance and moles or particles of a substance.

6.02 x 10²³ particles = 1 mol = molar mass

If we want to convert particles to mass, we must first convert particles to moles, and then we can convert moles to mass.

Example B3: What is the mass of 1.33 moles of titanium, Ti?

1. We want grams.

2. We have 1.33 moles of titanium.

3. Use the molar mass of Ti: 1 mol Ti = 47.88 g Ti.

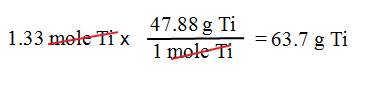
Atoms–Mass Calculation

Example B4: What is the mass of 2.55 x 10²³ atoms of lead?

1. We want grams.

2. We have atoms of lead.

3. Use Avogadro’s number and the molar mass of Pb.

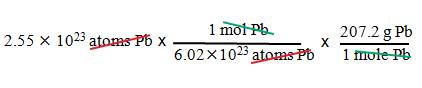
= 87.9 g Pb

Mass–Molecule Calculation

Example B5: How many F₂ molecules are present in 2.25 g of fluorine gas?

1. We want molecules F₂.

2. We have grams F₂.

3. Use Avogadro’s number and the molar mass of F₂.

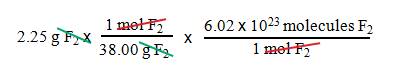
= 3.56 x 1022 molecules F₂

Mass of an Atom or Molecule

• What is the mass of a single molecule of sulfur dioxide? The molar mass of SO₂ is 64.07 g/mol.

• We want mass/molecule SO₂, we have the molar mass of sulfur dioxide.

• Use Avogadro’s number and the molar mass of SO₂ as follows:

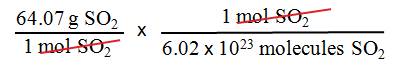
= 1.06 x 10^–22 g/molecule

Homework #3:

Calculate the mass in grams of 1.16 x 10²² molecules of nitrogen gas, N₂

Homework #4:

Calculate the number of entities in 0.641 g of oxygen gas, O₂

For part B additional problems may be found on page 245 #17-22.

Part C: Percent Composition 5 points

The percent composition of a compound lists the mass percent of each element.

For example, the percent composition of water, H₂O, is 11% hydrogen and 89% oxygen.

All water contains 11% hydrogen and 89% oxygen by mass.

Calculating Percent Composition of water

There are a few steps to calculating the percent composition of a compound. Let’s practice
using H₂O.

1. Assume you have 1 mol of the compound.
2. One mole of H₂O contains 2 mol of hydrogen and 1 mol of oxygen. Therefore,

2(1.01 g H) + 1(16.00 g O) = molar mass H₂O

2.02 g H + 16.00 g O = 18.02 g H₂O

3. Next, find the percent composition of water by comparing the masses of hydrogen and oxygen in water to the molar mass of water.

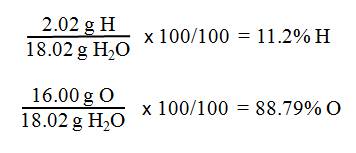
4. Remember: g H/100 g H2O is % H and g O/100 g H2O is % O

Example #2: Percent Composition Problem

TNT (trinitrotoluene) is a white crystalline substance that explodes at 240 °C. Calculate the percent composition of TNT, C₇H₅(NO₂)₃.

First calculate the molar mass of TNT

7(12.01 g C)

+ 5(1.01 g H)

+ 3 (14.01 g N + 32.00 g O) = g C₇H₅(NO₂)₃

84.07 g C

+ 5.05 g H

+ 42.03 g N

+ 96.00 g O

227.15 g C₇H₅(NO₂)₃

Second Calculate the % Composition

Module 5 Part C is covered in Section 8.7 of the textbook,  pages 235-236, calculating the Percent Composition of a Compound. Example 8.12 on page 236 demonstrates the process with a four element compound. You will calculate the Percent Composition of one compound on M-5 Exam.

Homework:

Calculate the percent composition of each element in the following compound:

Acetic Acid HC₂H₃O₂

There is an interactive web site that will allow you to check your work for Parts A & C. The author of ChemiCalc (which I posses two site licenses if you want a copy),  Dr. Bert Ramsay of Eastern Michigan University, has placed a small fraction of his program online. Check out:
http://people.emich.edu/bramsay1/ccc-release/chem.html

For additional examples at the end of the chapter do the Percent Composition on page 245 Questions #39-46

Part D: Empirical Formula Calculation 5 points

What is the Empirical Formula?

The empirical formula of a compound is the simplest whole number ratio of ions in a formula unit or atoms of each element in a molecule.

The molecular formula of benzene is C₆H₆.

- The empirical formula of benzene is CH.

The molecular formula of octane is C₈H₁₈.

- The empirical formula of octane is C₄H₉

Calculating Empirical Formulas from Lab Data

We can calculate the empirical formula of a compound from its composition data upon analysis in the lab.

We can determine the mole ratio of each element from the mass to determine the empirical formula of radium oxide, Ra_?O_?.

Example #1
A 1.640 g sample of radium metal was heated to produce 1.755 g of radium oxide. What is the empirical formula?

– We have 1.640 g Ra and 1.755 – 1.640 = 0.115 g O

– The molar mass of radium is 226.03 g/mol, and the molar mass of oxygen is 16.00 g/mol.

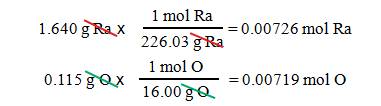
- We get Ra_0.00726O_0.00719.

- Simplify the mole ratio by dividing by the smallest number,0.00719 into both 0.00726 and .00719.

- We get Ra_1.01O_1.00

- Although we use at three significant figures throughout the calculation, empirical formulas are rounded to one significant figure resulting in whole number ratios

- Answer: RaO is the empirical formula

We will do a similar calculation in the lab: Determining the Empirical Formula

Calculating Empirical Formulas from % Composition

We can also use percent composition data to calculate empirical formulas.

• Assume that you have 100 grams of sample.

Acetylene is 92.2% carbon and 7.83% hydrogen. What is the empirical formula?

First: If we assume 100 grams of sample,
we have 92.2 g carbon
and 7.83 g hydrogen

Second: Calculate the moles of each element.

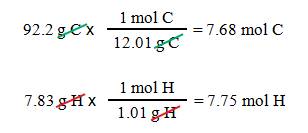
Third: The ratio of elements in acetylene is C_7.68H_7.75.

Fourth: Divide by the smallest number to get the following formula:

Homework #1 Empirical Formula via Lab Data:

In an experiment 2.410 gram of copper oxide produced 1.925 g of copper metal after heating with oxygen gas. What is the empirical formula of copper oxide?

Homework #2 Empirical Formula via % Composition:

Given the following percent compositions, determine the empirical formula of the following compound: 54.5% carbon, 9.15% hydrogen, and 36.3% oxygen

Module 5 Part D is a calculation of the Empirical and Molecular Formula from both the Lab Data and the Percent Composition which is described on pages 237-239.

Example 8.13, pages 237-238, demonstrates the process for calculation of empirical formula from lab data.

Example 8.14 page 239 demonstrates this process for the calculation from Percent Composition.

For Section 8.9 pages 239-240 You must know from this section what the difference is between an Empirical Formula and a true Molecular Formula of a compound and this will be tested in the Multiple choice section.

Section 11.10 is Hydrates. This section introduces the concept hydrates and Anhydrates which we may do as one of our M-5 crucible labs. Most crystalline salts come as hydrates, meaning water molecules are part of the crystalline structure. You should be able to interpret a hydrate formula where the dot between the two compounds reads "in combination with". CuSO₄ ∙ 5 H₂O reads one formula unit of CuSO₄ in combination with 5 molecules of water. Example 11.8 page 332 is a sample problem of interpreting the formula of a hydrate from lab data.

There are empirical formula problems at the end of the chapter to practice your empirical formula calculation of a compound: pages 246 problems #47-56.