CHM
1032C†††††††††††††††††††††††††††††††††† †Name: _________________
CHM
1032C Chapter 8: Gases, Liquids, and Solids
Chapter 8 Grading Outline
Chapter 8i: The Gaseous State† (Chapter 8) Close Book In-class Exam
A1._____(04) Properties of Solids (8.14), Liquids(8.12), and Gases 8.3 Answers
A.______(04) Kinetic Molecular Theory-Section 8.3 page220-221† Answers a
B.______(02) Discussion Real vs Ideal Gas Equation-lecture Answer bc
C.______(06) Standard Conditions/Molar Volume-Sect 8.3 p221 Answer bc
D.______(06) Gas Laws/Vocabulary-Sections 8.5, 8.6, 8.7, 8.8, 8.9, 8.10, 8.11 Answers
______(22) Module 6i Total (Twelfth Exam)
Chapter 8ii: The Gaseous State† (Chapter 8) Take-Home Exam
E.______(14) Gas Law Problems- Sections 8.5, 8.6, 8.7, 8.8, 8.9, 8.10, 8.11
Answers
F. ______(06) Enthalpy Change with
Phase Change Prob-Sect 8.15 Answer Sample 2
______(20) Chapter 8ii Total (Twelfth Exam)
Table
of Contents:
Chapter 8. Gases, Liquids, and Solids
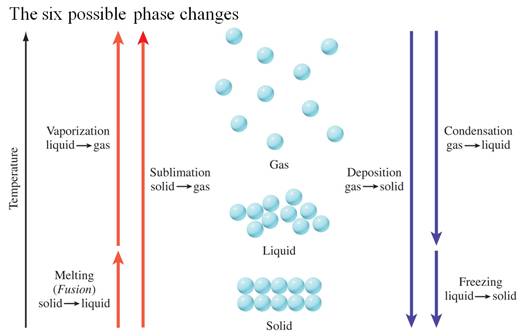
8.1 States of Matter and Their Changes
8.2 Intermolecular Forces
8.3 Gases and the KineticĖMolecular Theory
8.4 Pressure
8.5 Boyleís Law: The Relation between Volume and Pressure
8.6 Charlesís Law: The Relation between Volume and Temperature
8.7 Gay-Lussacís Law: The Relation between Pressure and Temperature
8.8 The Combined Gas Law
8.9 Avogadroís Law: The Relation between Volume and Molar Amount
8.10 The Ideal Gas Law
8.11 Partial Pressure and Daltonís Law
8.12 Liquids
8.13 Water: A Unique Liquid
8.14 Solids
8.15 Changes of State - See more at:
†
To begin your study of Chapter 8, please read Chapter 8 8
Part A: Kinetic Molecular Theory-Section 8.3
The gas properties and laws discussed
in Chapter 12 (Hein) are based on the Kinetic Molecular theory. The
CHM 1025C text list five (or six basic assumptions). You will write these
assumptions
1. Gases are composed of molecules*[1]. The distance
between the molecules is very-very great compared to the size of the
molecules themselves, and the total volume of the molecules is only a very-very
small fraction of the entire space occupied by the gas. Therefore,
considering volume, we are primary considering empty space.
(This assumption explains why gases are highly compressed and have very low
densities.)
(Gases are made up
of very tiny molecules. The volume of a gas is mainly empty space).
2. No attractive forces exist between molecules
in a gas.
(This is what keeps a gas from spontaneously becoming a liquid.)
(Gas molecules
have no attraction for one another.)
3. The molecules of a gas are in a
state of constant, rapid motion, colliding with each other and with the
walls of the container in a perfectly random manner. (This assumption explains why
different gases normally mix completely. The collisions between molecules
and the walls of the container account for the pressure exerted by the gas.)
(Gas molecules
demonstrate rapid motion, move in straight lines, and travel in random
directions.)
4. All of these molecular collisions are perfectly elastic.
As a result, the system as a whole experiences no loss of kinetic
energy, the energy derived from the motion of a particle.
(Gas molecules
undergo perfect elastic collisions.)
5. The average kinetic energy per molecule of a gas is
proportional to the absolute temperature, and the average kinetic energy per
molecule is the same at a given temperature and pressure for all gases.
(The average kinetic energy of gas molecules is proportional to the
Kelvin temperature, that is KE is approximately T.)
When we think
of molecules of elemental gases, we usually think of the diatomic gases such as
nitrogen, oxygen, hydrogen, etc. The Nobel gases exist as monoatomic
gases such as Helium, Neon, etc.
Some† texts reduce these assumptions to three, these assumptions are
condensed as follows:
(a) Gases consist of
particles (molecules or atoms), whose separation is much greater than the size
of the particles themselves.
(b) The particles of a
gas are in continual, random, and rapid motion. As they move, they collide with
one another and with the walls of their container, but they do so without
energy loss.
(c) The average kinetic
energy of gas particles is proportional to the gas temperature. All gases,
regardless of molar mass, have the same average kinetic energy at the same
temperature.
Module Six- Part A: Kinetic Molecular Theory††† 2 points
†State the 5
assumptions of the Kinetic Molecular theory as stated in the book (Section 8.3) :
1
2
3
4
5.
Chapter
8 Homework Packet-Page 2
Chapter
8 A1 Properties of Solids, Liquids and Gases† 3 Points
State
four of the five properties of solids:
a.
b.
c.
d.
e.
State
four of the five properties of liquids :
a.
b.
c.
d.
e.
State
four of the five properties of gases :
a.
b.
c.
d.
e.
Chapter
8 Homework Packet Ė Page 3
Part B: Discussion Real vs Ideal Gas Equation
If you have an understanding of the
Kinetic Molecular Theory above then when you read in a college chemistry text† you apply the
KMT to gases in non ideal behavior. At STP gases behave ideally. But under
extreme conditions which cause overcrowding (what are these conditions?), the
KMT breaks down such that the Ideal gas Equation: PV=nRT
has to be re-written to the Real Gas Equation. This leads to the following
discussion questions:
(a) In
the Real Gas Equation: (P + an2/V2) (V - nb) = n RT a pressure correction factor was added. Why? (What
assumptions of the kinetic theory breakdown under extreme conditions of
temperature and pressure?)
(b)
Also a volume correction factor was subtracted. Why? (What assumptions of the
KMT breakdown under extreme conditions?)
Another
assumption of the kinetic molecular theory is that collisions between the
molecules are elastic-that is, that the atoms or molecules of the gas never
stick to one another by some type of intermolecular force. This is not
true at extreme conditions of overcrowding. When a molecule is about to strike
the wall of its container, other molecules in the vicinity exert a slight
attraction for the molecule and pull it away from the wall. As a result of the
intermolecular forces, molecules strike the wall with less force than they would
in the absence of intermolecular attractive forces. Therefore, in a real gas,
the observed pressure is less than the predicted pressure by the ideal gas law
and a pressure correction factor is added to account for this pressure loss.
Also a
volume correction factor was subtracted. Why? (What assumptions of the KMT
breakdown under extreme conditions?)
The kinetic
molecular theory and the ideal gas law are concerned with the volume available
to the molecules to move about, not the volume of the molecules themselves. It
is clear the volume occupied by the gas molecules is NOT negligible at high
pressures (or extreme low temperatures. The available volume is less than the
volume of the container. The volume the molecules occupy must be subtracted
from the volume of the container to obtain the volume of free space the
molecule can move.
A good multiple choice question
is: under what conditions does ideal gas behavior break down?
Module Six Part B: Discussion Question (2 points)
In the Real Gas Equation:††
(P + an2/V2) (V - nb) = n RT a pressure correction factor was added. Why?
(What assumptions of the kinetic theory breakdown under extreme conditions of
temperature and pressure?)
Also a volume correction factor was subtracted. Why? (What assumptions
of the KMT breakdown under extreme conditions?)
Part C: Standard Conditions/Molar Volume-
Properties of gases are
discussed. This includes the introduction to the concept of Gas pressure. Here
is a summary:
1.
Gases have indefinite shape
2.
Gases can expand
3.
Gases can compress
4.
Gases have low density
5.
Gases mix completely with other gases in the same container.
†Atmospheric Pressure is discussed in Section
8.4. The pressure that a gas exerts depends on how often and how hard these
molecules strike the walls of the container:
1. If the molecules
collide more often, the gas pressure increases.
2. If the molecules collide with more energy, the
pressure increases.

Table 12.2 from another book lists the units of gas pressure
under standard conditions:

State standard conditions (STP) in three units of pressure (the
last is your choice) and oC and K
temperatures:
 †
†
_760__mmHg or _760__torre=
__1___atm = _29.9 in_ = _14.7 psi_= 101 kPa
__0_oC
= _273__K
You should know the value of the gram molar
volume constant to three significant figures. 
Therefore you would put 22.4
in any of the following blanks:
What
are the values for the Molar Gas Volume Constant for the following gases:
1 moleCO2 =__22.4__L CO2@STP
1 moleH2
=__22.4___L H2@STP
1 moleN2 =__22.4___L N2@STP
1 moleO2
=__22.4___L O2@STP
Calculate
the value of R in the Ideal Gas Equation at STP:
If you substitute the
values of the Molar Gas Constant into the ideal gas equation (PV=nRT) you can calculate the value of the constant R:
PV
= nRT (you must enter Kelvin temperatures-not Celsius)
(1 atm)
(22.4 L) = (1 mole) R (273 K)
R = 0.08206 L atm/mol K
R can
include energy units such as Joules or calories:
|
Values for the gas constant R |
|
|
Units |
Value |
|
L atm/mol K |
0.08206 |
|
cal/mol K |
1.987 |
|
J/mol K |
8.314 |
|
m3 Pa/mol K |
8.314 |
|
L torr/mol K |
62.36 |
We usually use the first
value: 0.08206 (or 0.0821) L atm/mol K in the
calculation in Chapter 8. However, many times your pressure is not given in
atmospheres and if you do not have the above table, you may have to make conversions
of the units of pressure from one unit to another. Here are a few example
problems:

These calculation may be in multiple choice questions.
Chapter 8
-Part C††† Standard Conditions/Molar
Volume†††† 2 points
State standard conditions (STP) in three units of pressure
(the last is your choice) and oC and K temperatures:
_____mm Hg or ______torre=† ______atm =† _____†† ______(you write the unit too)
_____ oC†† =††† ______K
Are the values for the Molar Gas Volume Constant:
1 mole CO2 =________L
CO2@STP†††††† 1 mole
H2 =________L H2@STP
1 mole N2 =________L
N2@STP††††††††††† 1 mole
O2 =________L O2@STP
Module Six-Part C1: Gas
Pressure Calculations††† 2 points
The average
barometric pressure at an altitude of 10 km is 210 torre.
Express
this pressure in:
(a) Atmospheres
(b) Bars
(c) Kilopascals
(d) In
Hg
(e) mmHg
Module Six-Part C2: Value of
R††† 2 points
Given
the Molar Gas Constant in Part C, Determine the value of R
in the
ideal gas equation
(a) †using first atmospheres
(b) †Using torre
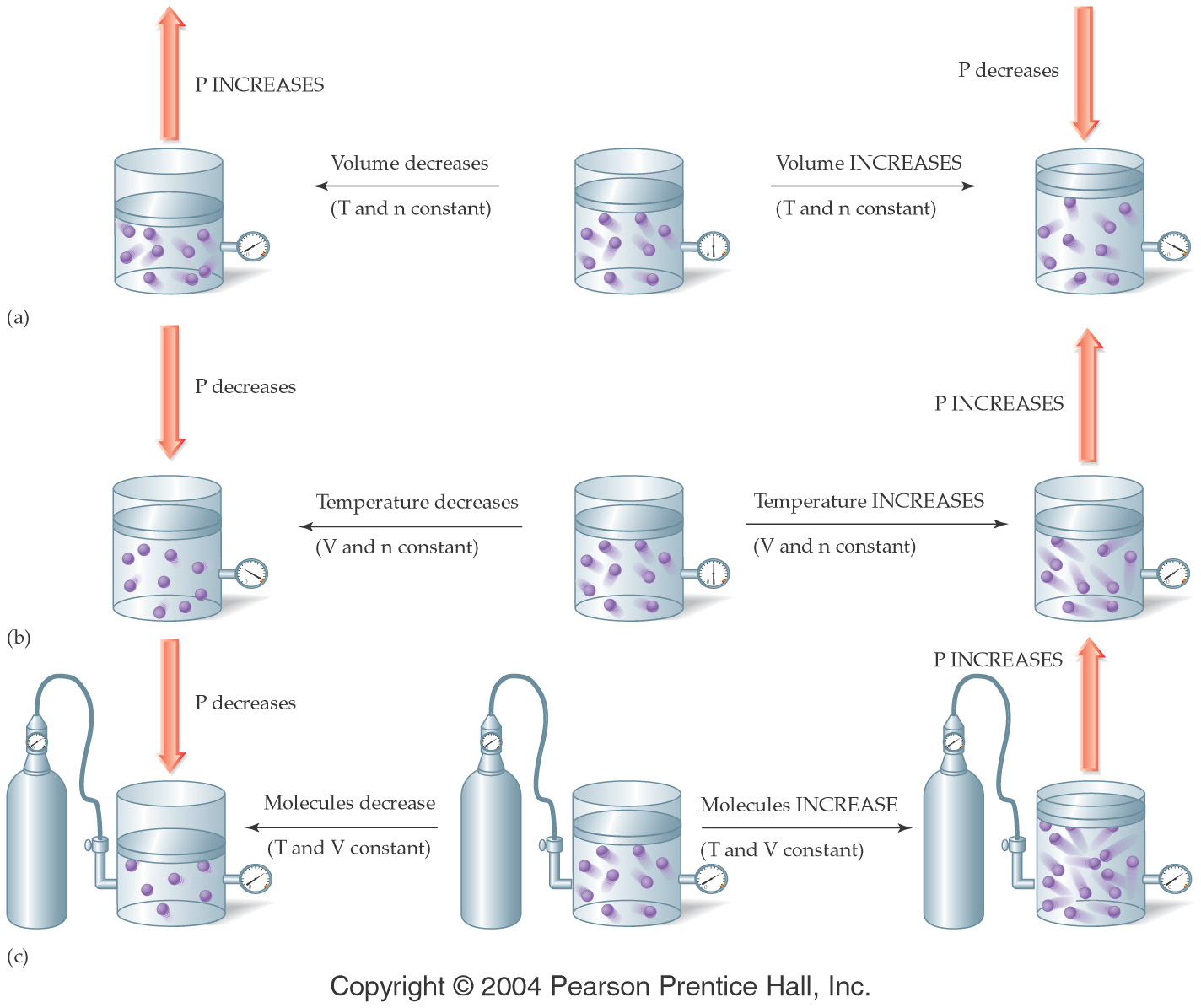
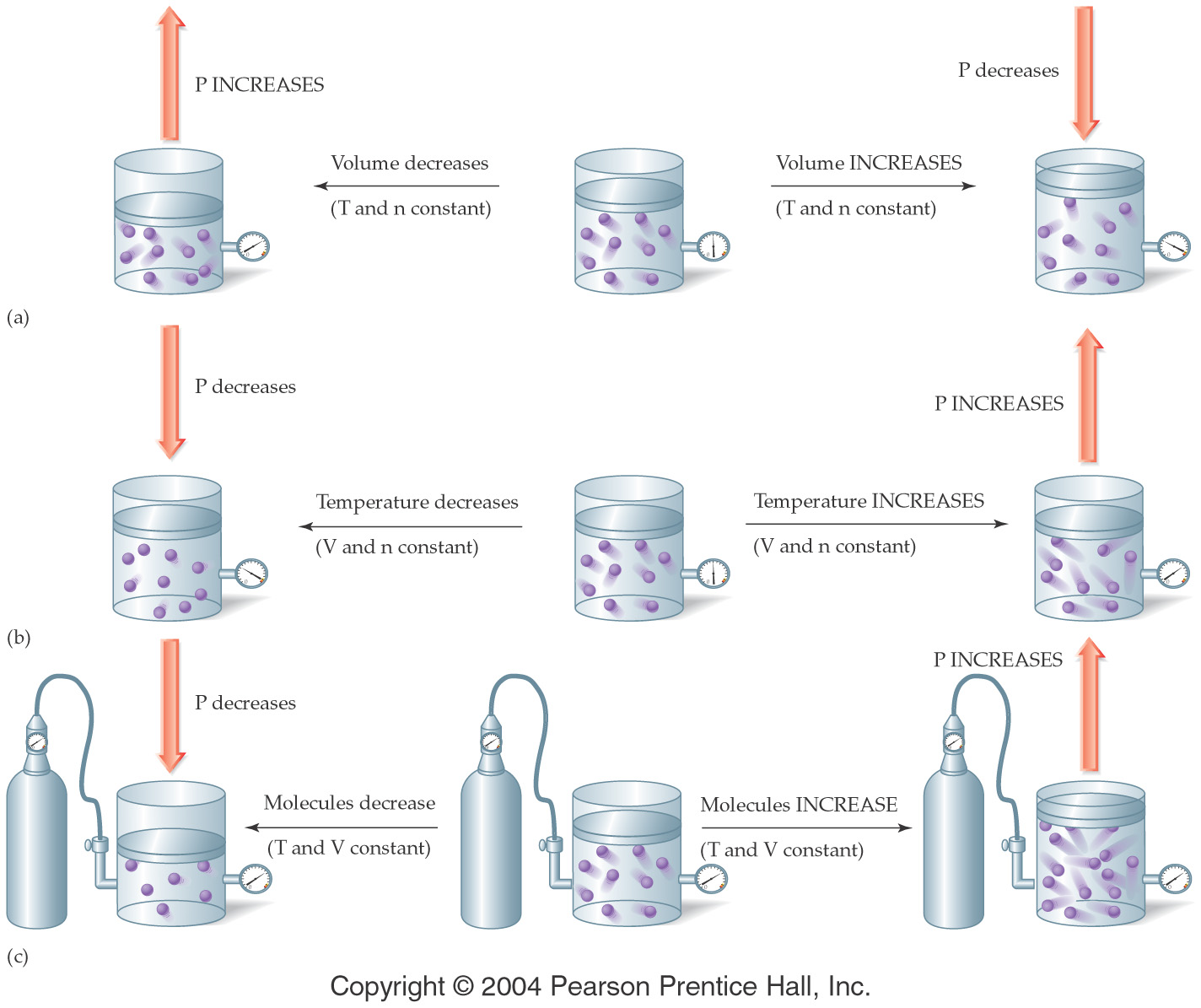
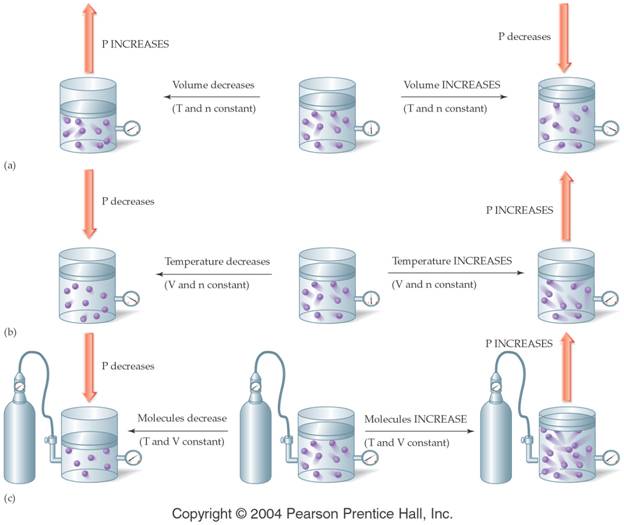
Part D: Gas Laws/Vocabulary-
In
sections of another book 12.2-12.7 Variables affecting gas pressure are best described
by the following figure:
†
†For Part D you simply write a
statement of the gas laws covered in chapter 8 section 8.5 Boyle's Law,
Section 8.6 Charles Law-, Section 8.7 Gay-Lussacís Law , Section 8.9 Avogadroís
Law is defined;† Section 8.8 Combined Gas
Law and Section 8.10 the Ideal Gas Equation is covered in Section 8.8.† Daltonís law is covered in Section 8.11,
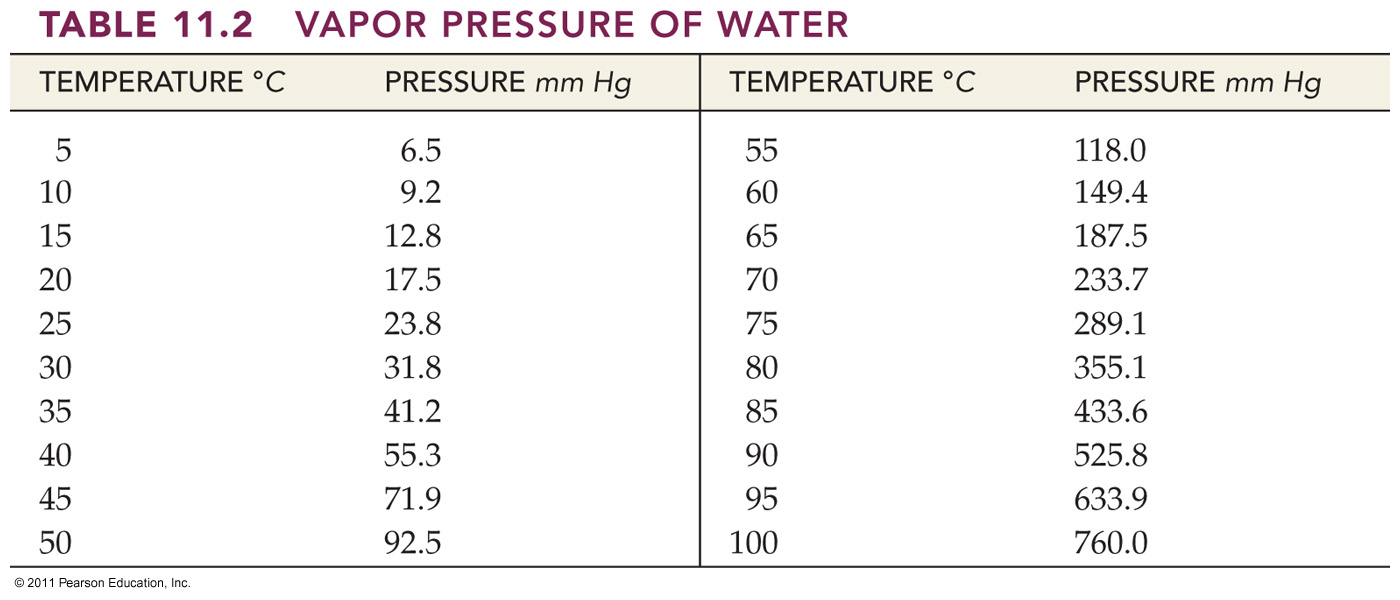
while Vapor pressure Concept is covered in Section 8.12.
† Here are the statements:
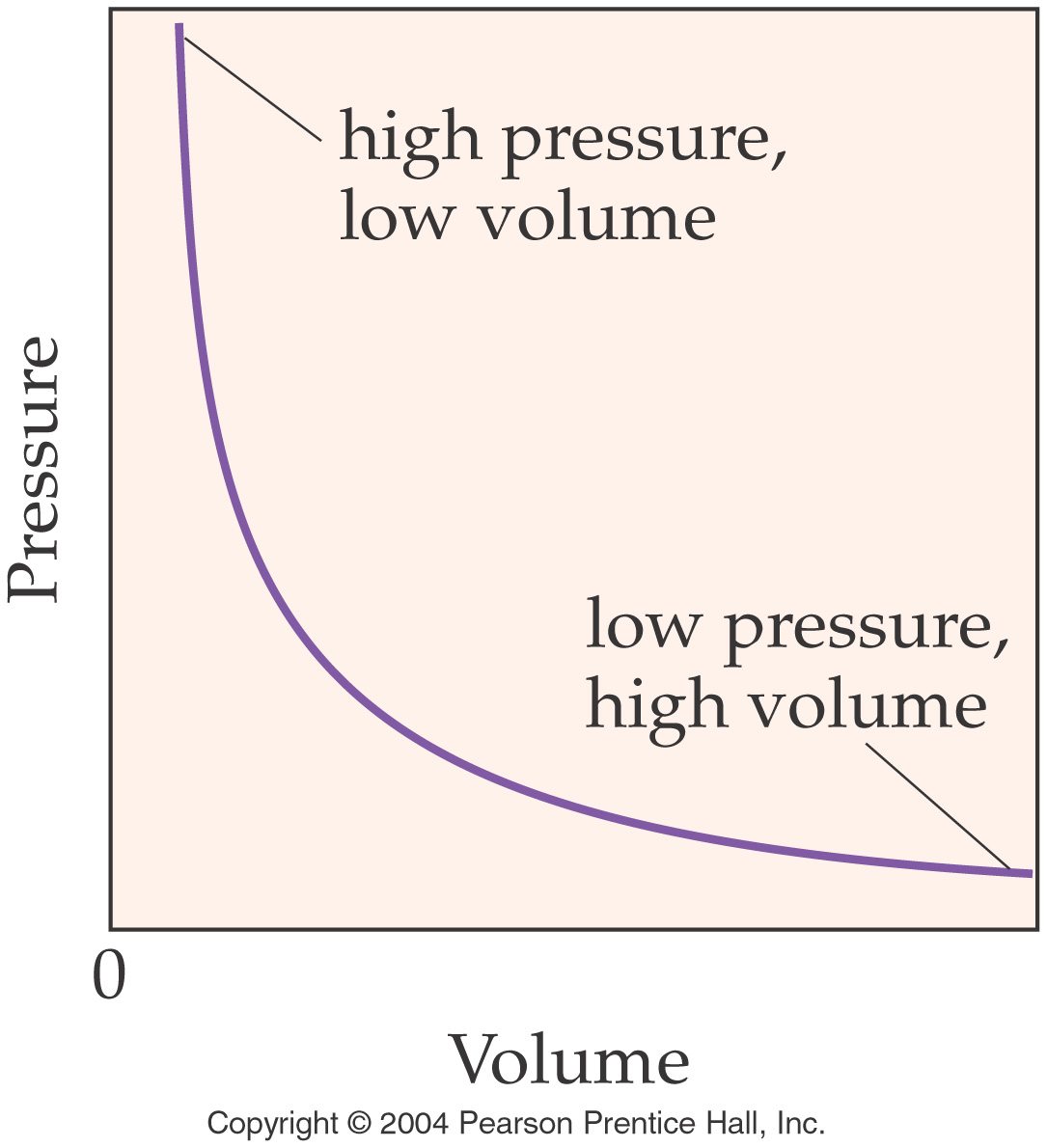
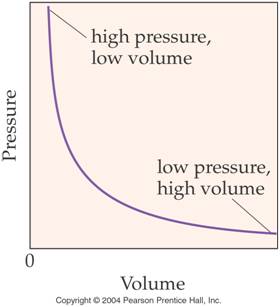
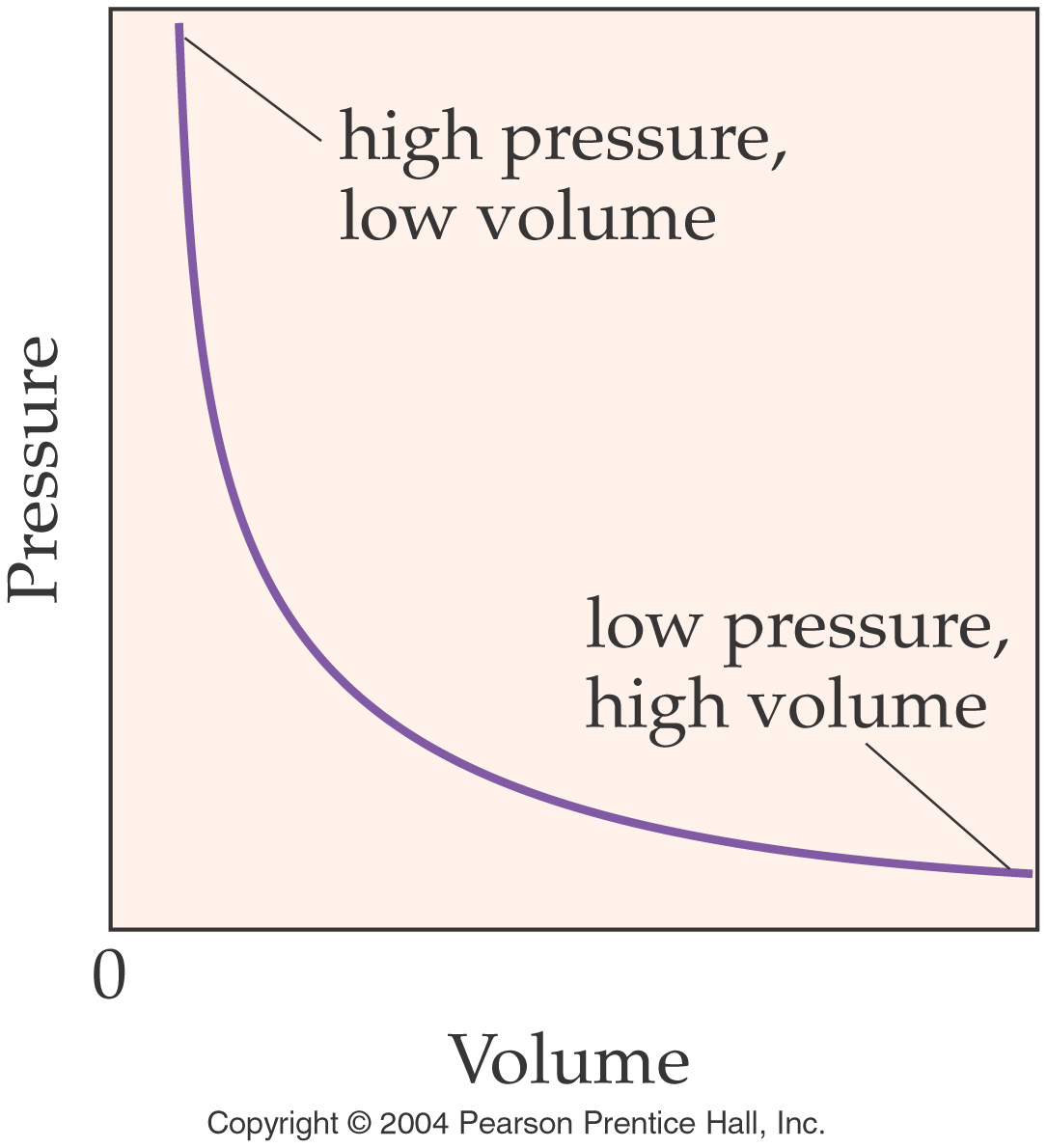
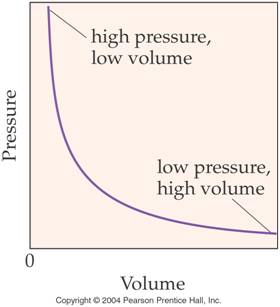
Boyleís Law (In words) Section 8.5
pages 225-228
The volume of a gas is inversely proportional to the pressure when
the temperature remains constant.
V1P1=V2P2
Note the graphical relationship
between Pressure and Volume:

Below is another set of worked
examples not in your book:
†


Charles Law (in words) ††††Section 8.6
The volume of a gas is directly proportional to the Kelvin temperature
if the pressure remains constant.
†V1† =† V2
T1††††† T2
Note the graphical relationship
between Temperature and Volume:

Why does the first graph
not interest the origin, while the second one does?
Here is another worked example not in your book:

Gay-Lussacís Law (in words) ††††Section 8.7
The pressure of a gas is directly proportional to the Kelvin
temperature if the volume remains constant.
P1† =† P2
T1††††† T2
Note the graphical relationship between Temperature and
Pressure:

It looks the same as Charles
Law. Why?

Study Example 10.5 page 292 for a sample
problem for Part E.† You should try
Problems #29-32 at the end of the chapter on page 308 for additional Part E
type problems.
Daltonís Law of Partial
Pressures (in words)† Section 8.11
The total pressure of a
gaseous mixture is equal to the sum of the individual pressure of each gas.
Ptotal =† P1† + P2† + P3 + Ö
Define
Vapor pressure: Vapor pressure is the pressure exerted
by the gaseous vapor above a liquid (usually in a closed container) when the
rates of evaporation and condensation are equal.†
††††††  ††††††††††††††††††
††††††††††††††††††
.
Here are more examples of work
Daltonís law application which are not in our book:


From Another book:

Avogadroís Law (in
words/formula) ††††Section 9.9
The volume of a gas is directly proportional to the number of
molecules (moles) if the pressure and temperature remain constant.
†V1 †=† V2
n1†††††† n2
Avogadroís Law Calculation

Combined Gas Law Equation (write only the equation):

Derive the combined gas law from the
Ideal Gas Equation: PV = nRT:
V1P1†† =†† V2P2
† T1†††††††††† T2
Study example 10.6 pages 294-295 for a
sample Part E Problem.
Work examples at the end of the
chapter Page 308 #33-42
Ideal Gas Equation (write only the equation):
Section 8.10 McMurry


Rearrange to for the Ideal gas Equation:
PV = nRT



Chapter 8
Part D Gas Laws†††††††††††††††††††††††††††††††††††††††† 4
points
State:
Boyleís Law (In words and formula) (See Section 9.2)
Charles Law (in words and formula) (See Section 9.2)
Daltonís Law of Partial pressures (in words and formula)
(See Section 9.5)
Gay-Lussacís Law (in words and formula) (not in McMurry)
Avogadroís Law (in words and formula) (Section 9.2)
†
Combined Gas Law Equation (write only the equation)
Ideal Gas Equation (write only the equation) (See Section
9.3)
Define Vapor Pressure (See Section 10.8):
Grahamís Law of Diffusion and Effusion-Section 9.7
Chapeter 8† Part E Gas Law Problems††††††††††††††††††††††††††† 14 points
Boyleís Law
1.† A sample of a gas has a volume of 100 mL when measured at 25 oC
and
†760 mmHg.† What volume will the gas occupy at 25 oC and 380 mmHg?
Charles Law(
. The volume of a gas is 100.0 mL
at 27 oC.† At what temperature in degrees Celsius would
the volume of the gas be 200.0 mL, assuming the
pressure remains constant.
Gay-Lussacís Law
3.† A sample of gas
occupies 100.0 L at 710.0 torre and 27 oC.†
Calculate the pressure in torre if the
temperature is changed to 127 oC
while the volume remains constant.
Daltonís Law of Partial Pressures
4. Calculate the dry volume in milliliters of 200 mL of hydrogen gas collected over water at 25 oC at 760 torre
pressure with the temperature remaining constant.† (The partial pressure of water vapor at 25 oC is 23.8 torre.)
Avogadroís Law
5.†† A 1.5 mole sample
of a gas occupies 25.0 L at 758 torre and 27oC.
Calculate the Volume of the gas, if more molecules are injected into the vessel
increasing the moles to 2.5 moles, provided the pressure and the temperature do
not change.
Combined Gas Laws
6. A100.0 mL sample of air is
collected at 25oC and 774 mmHg. What is the volume at STP?
†
Ideal Gas Equation
7. Calculate the number of moles of nitrogen gas in a 5.00 L
cylinder at 27 oC and 4 atm pressure. R = 0.0821 L atm/ K
mole )
How much does this volume of gas weigh?

Part F: Enthalpy Change with Phase Change



Chapter 8 Section 8.15
Part D: Enthalpy change with Phase Change/Ice
Cube Problem††
†Phase
Change (3 points):
1.
Calculate the amount of heat necessary to melt 27.0 grams of ice at 0oC, if the heat of fusion of ice is 333 J/g.
†If I had the same amount of water at 100oC,
calculate the amount of heat required to boil 27.0 grams of water if the heat of vaporization of water is 2256 J/g?
†How much heat is required to raise the
temperature of the 27 grams of water at
0oC to 100oC, if the specific heat of water is 4.184 J/goC
Ice Cube Problem (2 points):
If 27.0 grams of ice at 0oC is added
to an insulated cup of water containing
123 grams of water at 50oC. What will be the final thermodynamic
equilibrium temperature of the water/ice mixture assuming no heat is lost to the
surroundings?